누적 합

배열의 [a, b] 구간의 합을 구할 때, 구간에 속하는 값을 각각 더하는 연산은 시간 복잡도 O(n)으로 매우 느리다. 크기가 작은 구간합을 한 번만 구하는 경우에는 문제가 없지만, 크기가 크거나 구간합을 여러 번 구할 경우 매우 느리기 때문에 다른 방법을 사용해야 한다.

배열의 0번째 성분부터 k번째 성분을 더한 값을 sum[k]라고 하자. 구간 [a, b]의 합은 곧 a부터 b까지 더한 값이므로, 1부터 b까지 더한 값에 1부터 a - 1까지 더한 값과 같다. 이 값은 sum[b] - sum[a - 1]과 같으므로, 구간 [a, b]에서의 합은 곧 sum[b] - sum[a - 1]과 같다. 이 방법을 사용하면 sum을 만들 때의 시간복잡도가 O(n)이 되지만, 이후 구간합을 구할 때의 속도가 O(1)이므로 긴 구간의 합을 자주 구해야 할 때 사용할 수 있다.

int arr[LEN], sum[LEN];

void make_sum() {
    sum[0] = arr[0];
    for (int i = 1; i < LEN; i++) sum[i] = sum[i - 1] + arr[i];
}

int get_sum(int a, int b) { return sum[b] - sum[a - 1]; }

위 방법은 부분합을 구하는 것이 매우 쉽고 빠르다는 장점이 있지만, sum을 재계산할 때의 시간 복잡도가 O(n)이므로 배열의 성분이 자주 바뀌는 경우 사용할 수 없다는 문제점이 있다. 이럴 때 사용하는 것이 바로 펜윅 트리인데, 펜윅 트리는 인덱스에 비트 연산자를 사용해 부분합과 갱신 모두 시간 복잡도가 O(log2(n))인 이진 트리를 말한다.

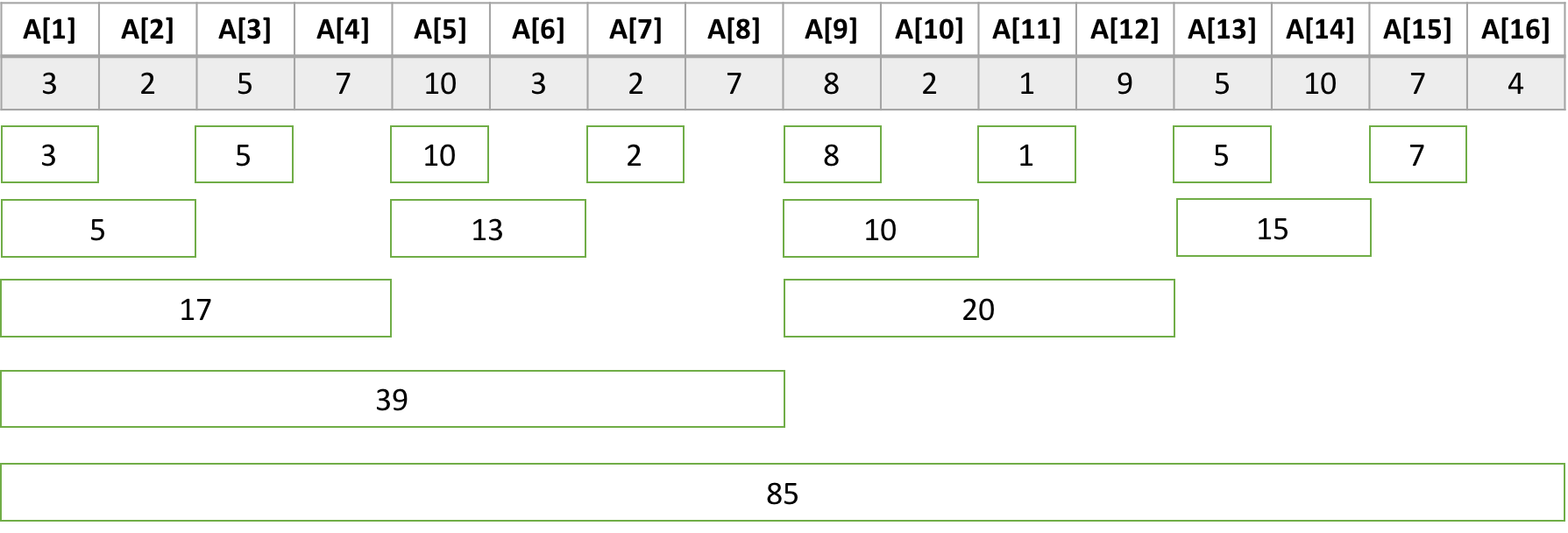
펜윅 트리를 이해하기 위해선 우선 컴퓨터에서 정수가 이진법으로 표현된다는 점을 알아야 한다. 위 이미지를 보면 배열의 5번째 성분이 펜윅 트리의 5, 6, 8, 16번째 성분에 포함되어 있음을, 11번째 성분은 11, 12, 16번째 성분에 포함되어 있음을 알 수 있는데, 이 인덱스 집합을 구하는 방법이 바로 이진법을 활용하기 때문이다. num번째 성분에 값을 업데이트 한 뒤, 다음으로 업데이트 할 인덱스는 num을 이진법으로 나타냈을 때 자리수가 가장 작은 1을 더한 값인데, 이 값은 (num & -num)로 나타낼 수 있다.

      -num = ~num + 1
       num = 100110101110101100000000000
      ~num = 011001010001010011111111111
      -num = 011001010001010100000000000
num & -num = 000000000000000100000000000

펜윅 트리로 부분합을 구하는 방법은 위의 sum[b] - sum[a - 1]과 같은데, 그렇다면 펜윅 트리에서 부분합 [1, num]은 어떻게 구할까? 답은 업데이트할 때와 같이 (num & -num)을 사용하는 것인데, 업데이트할 때는 num에 해당 값을 더했다면 부분합을 구할 때는 해당 값을 빼야 한다. 예를 들어 num이 13이라면 부분합은 펜윅 트리의 13번, 12번, 8번 값을 더해 얻을 수 있는데, 이 값을 각각 이진법으로 나타내면 1101, 1100, 1000이므로 자리수가 가장 작은 1이 0으로 점점 변함을 알 수 있다.

int arr[LEN + 1] = { 0, }, fenwick[LEN + 1] = { 0, };

void set(int num, int val) {
    val -= arr[num];
    arr[num] += val;

    while (num < N) {
        fenwick[num] += num;
        num += num & -num;
    }
}

int get(int num) {
    int ret = 0;

    while (num) {
        ret += fenwick[num];
        num -= num & -num;
    }

    return ret;
}