트리는 그래프의 특수한 형태로, N개의 노드에 N - 1개의 에지만이 존재하고, 두 노드 i와 j에 대해 그 경로가 단 한 가지만 존재하며, 에지의 방향이 존재하지 않는다.
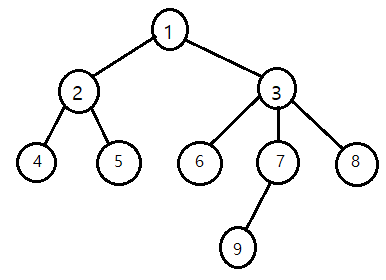
트리는 그래프에 없는 몇 가지 특징을 가지고 있는데, 우선 트리는 한 점에서 뻗어나가듯 시작된다는 것이다. 위 이미지를 보면 트리가 1번 노드에서부터 시작하는 모양을 하고 있는데, 이러한 노드를 루트 노드라고 부른다. 또한 1번은 아래에 2번 노드와 3번 노드를, 2번 노드는 아래에 4번 노드와 5번 노드를 가지고 있는데, 이렇게 서로 인접한 노드 중 루트 노드에 더 가까운 노드를 부모 노드, 그렇지 않은 노드를 자식 노드라고 부른다. 위 이미지의 4번 노드와 9번 노드처럼 자식 노드가 없는 노드를 리프 노드라고 부르고, 루트 노드에서 리프 노드까지 이동할 때 필요한 에지의 최댓값을 높이라고 부른다. 또 트리의 어느 노드 i에 대해 노드 i의 부모 노드와 그에 연결된 모든 노드를 무시하면 노드 i를 루트 노드로 하는 트리만 남는데, 이러한 구조는 서브 트리라고 부른다.
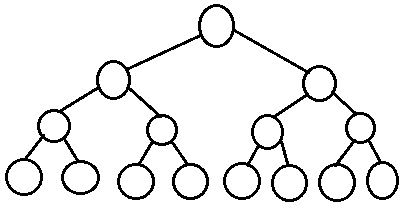
알고리즘 문제풀이에서 주로 사용되는 형태는 이진 트리라는 형태인데, 1차원 배열을 이용해 나타낼 수 있기 때문이다. 루트 노드의 인덱스를 1이라고 하고, 어떤 노드의 인덱스가 i일 때 노드 i의 두 자식 노드의 인덱스를 2 * i, 2 * i + 1로 나타낸다면 부모 노드의 인덱스는 i / 2가 되므로 모든 노드의 인덱스가 겹치지 않게 트리를 표현할 수 있기 때문이다.
이진 트리를 순회하는 방법은 전위 순회, 중위 순회, 후위 순회 세 가지 방법이 있는데, 세 방법 모두 왼쪽 노드를 탐색한 다음 오른쪽 노드를 탐색한다. 세 방법이 다른 점은 루트 노드를 탐색하는 순서인데, 전위 순서는 왼쪽 노드를 탐색하기 전에, 중위 순회는 왼쪽 노드를 순회하고 오른쪽 노드를 순회하기 전에, 후위 순회는 오른쪽 노드를 순회한 후에 루트 노드를 탐색하게 된다.