https://www.acmicpc.net/problem/2873
2873번: 롤러코스터
첫째 줄에 가장 가장 큰 기쁨을 주는 롤러코스터는 가장 왼쪽 위 칸부터 가장 오른쪽 아래 칸으로 어떻게 움직이면 되는지를 출력한다. 위는 U, 오른쪽은 R, 왼쪽은 L, 아래는 D로 출력한다. 정답
www.acmicpc.net
주어지는 입력의 경우를 R이 홀수일 때, C가 홀수일 때, R과 C 둘 다 짝수일 때로 나눠보자. R이 홀수일 때와 C가 홀수일 때는 모든 칸을 지날 수 있음이 자명하므로, 이 문제를 풀기 위해선 R과 C 모두 짝수일 때 기쁨 지수의 합의 최대치를 구하는 방법이다.
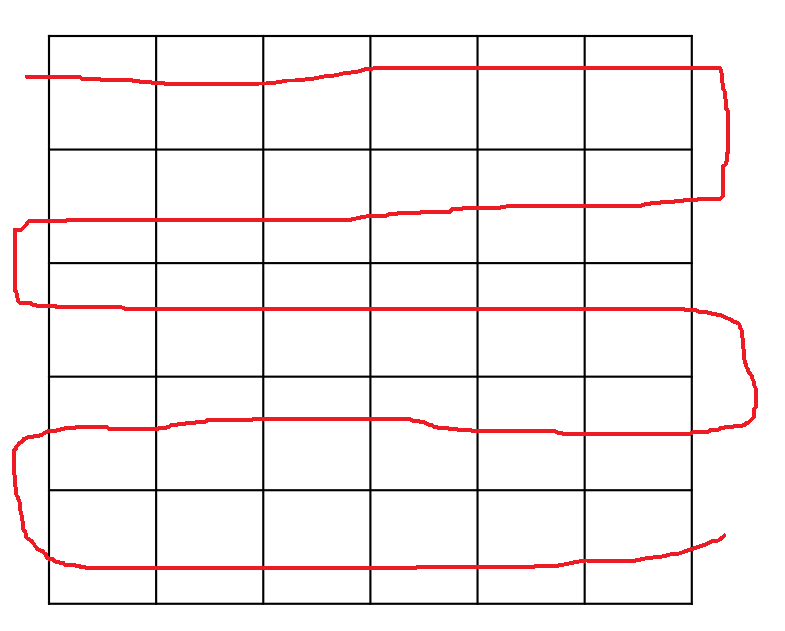 R이 홀수인 경우 각 행을 차례로 탐색한다 |
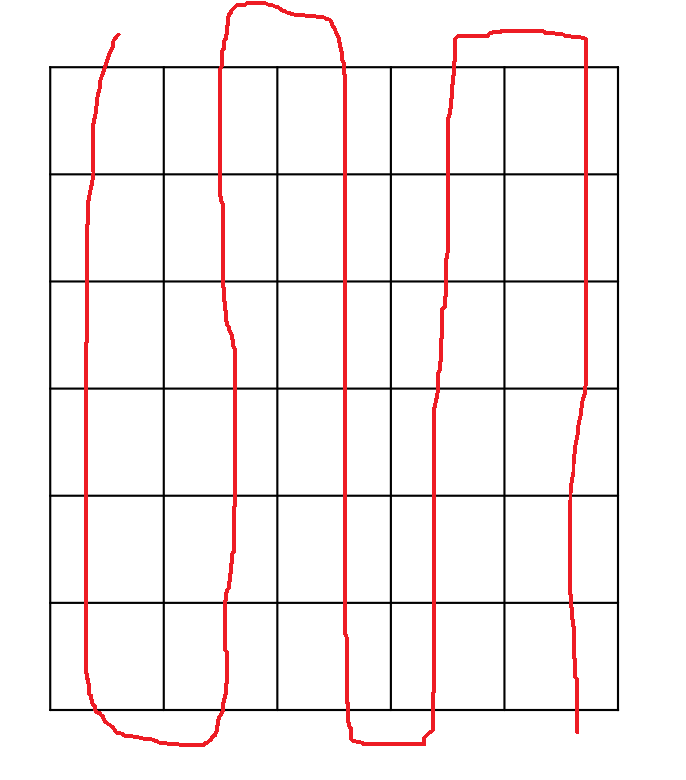 C가 홀수인 경우 각 열을 차례로 탐색한다 |
롤러코스터의 각 칸의 좌표 (i, j)에 대해, (i + j)가 짝수인 칸 하나를 방문하지 않고 넘기기 위해선 그 인접한 칸, 즉 (i + j)가 홀수인 칸을 하나 이상 방문하지 않아야 한다. 하지만 (i + j)가 홀수인 칸 하나를 방문하지 않고 넘길 때, 다른 칸을 모두 방문할 수 있는 방법은 반드시 존재하므로 기쁨 지수의 합이 최대가 되기 위해선 (i + j)가 홀수이고 기쁨 지수가 최소인 칸 p(i, j)를 건너뛰어야 한다.

건너뛸 칸 p(i, j)를 건너뛰는 방법을 출력하기 위해 0번째 행과 1번째 행, 2번째 행과 3번째 행, ..., R - 2번째 행과 R - 1번째 행을 묶자(이 때 R은 짝수이므로 남는 행은 존재하지 않는다). 이렇게 묶은 행 집합 중 p를 포함하지 않은 행 집합은 R이 홀수일 때와 같은 방식으로 출력할 수 있다.
p가 속하는 행 집합을 C / 2개의 2 * 2 블록 집합으로 나누자(이 때 C는 짝수이므로 남는 블록은 존재하지 않는다). 맨 왼쪽 블록 집합부터 p가 속하는 블록 집합 직전까지는 왼쪽 위에서 시작해 오른쪽 위에서 끝나도록 각 블록 집합의 모든 블록을 탐색하고, p가 속하는 블록 집합 직후부터 맨 오른쪽 블록 집합까지는 왼쪽 아래에서 시작해 오른쪽 아래에서 끝나도록 각 블록 집합의 모든 블록을 탐색하면 p가 속하는 행 집합을 거의 모두 탐색할 수 있다.
p가 속하는 블록 집합에 대해, p의 좌표 (i, j)에 대해 (i + j)는 홀수이고, 블록 집합의 왼쪽 위 좌표 (a, b)에 대해 (a + b)는 짝수이다. 따라서 p는 블록 집합의 왼쪽 아래, 혹은 오른쪽 위에 위치한다. 이 때 p가 블록 집합의 왼쪽 아래에 위치한다면 해당 블록을 탐색하는 방법은 DR이고, 오른쪽 위에 위치한다면 탐색하는 방법은 RD가 된다. 따라서 p가 속한 블록을 해당 방식으로 탐색한다면, 롤러코스터에서 좌표 (i, j)에 대해 (i + j)가 홀수이고 기쁨 지수가 최소인 한 점을 제외한 모든 점을 탐색 가능하다.
#include <iostream>
using namespace std;
#define MAX_R 1000
#define INF 0x3f3f
int main() {
// 입출력 속도 향상
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
// 롤러코스터의 행/열이 모두 짝수라면 true, 아니라면 false
bool is_even;
// R, C: 롤러코스터의 행/열의 수, val[i][j]: i행 j열의 기쁨 지수
// p, min: 스킵 가능한 지역의 좌표와 기쁨 지수의 최소치
short R, C, val[MAX_R][MAX_R], p[2] = {0, 1}n = INF;
// 롤러코스터의 행/열의 크기를 입력받은 뒤 그 둘이 모두 짝수인지를 저장
cin >> R >> C;
is_even = (R % 2 == 0) && (C % 2 == 0);
// 롤러코스터의 각 지역을 입력받으면서
for (int i = 0; i < R; i++) for (int j = 0; j < C; j++) {
cin >> val[i][j];
// 해당 지역이 스킵 가능하며 기존 스킵 지역보다 기쁨 지수가 작다면
if (is_even && (i + j) % 2 && min > val[i][j]) {
// 스킵할 지역을 현재 지역으로 갱신
min = val[i][j];
p[0] = i;
p[1] = j;
}
}
// 행의 수가 홀수라면 각 을 차례로 탐색하는 것으로 모든 칸을 탐색 가능
if (R % 2 == 1) {
for (int i = 0; i < (R / 2); i++) {
for (int j = 1; j < C; j++) cout << 'R';
cout << 'D';
for (int j = 1; j < C; j++) cout << 'L';
cout << 'D';
}
for (int j = 1; j < C; j++) cout << 'R';
}
// 열의 수가 홀수라면 각 열을 차례로 탐색하는 것으로 모든 칸을 탐색 가능
else if (C % 2 == 1) {
for (int i = 0; i < (C / 2); i++) {
for (int j = 1; j < R; j++) cout << 'D';
cout << 'R';
for (int j = 1; j < R; j++) cout << 'U';
cout << 'R';
}
for (int j = 1; j < R; j++) cout << 'D';
}
// 행과 열의 수가 모두 짝수라면 좌표 (i, j)에 대해
// (i + j)가 홀수인 한 칸을 제외한 모든 칸을 탐색 가능
else {
// 행 단위로 탐색하기 위해 두 행을 하나로 묶은 뒤
// 스킵할 칸 p가 있는 행 쌍에선 특수한 이동 방식을 취하고
// 나머지 행은 단번에 탐색
is_even = !(p[0] % 2); p[0] /= 2;
// p가 있는 행 쌍 이전의 모든 행을 순차적으로 탐색
for (int i = 0; i < p[0]; i++) {
for (int j = 1; j < C; j++) cout << 'R';
cout << 'D';
for (int j = 1; j < C; j++) cout << 'L';
cout << 'D';
}
// p가 있는 행 쌍을 2 * 2 칸으로 묶은 뒤
// p가 속하지 않은 2 * 2칸의 모든 칸을 차례로 탐색한 뒤
for (int i = 0; i < p[1] / 2; i++) cout << "DRUR";
// p가 속한 2 * 2 칸에서 p 이외의 칸을 탐색한다
// 이 때 p[0]이 짝수라면 p는 2 * 2의 오른쪽 위, 홀수라면 왼쪽 아래에 있다.
cout << (is_even ? "DR" : "RD");
// p가 속하지 않은 2 * 2칸의 모든 칸을 차례로 탐색한다
for (int i = (p[1] / 2) + 1; i < C / 2; i++) cout << "RURD";
// p가 있는 행 쌍 이후의 모든 행을 순차적으로 탐색
for (int i = p[0] + 1; i < R / 2; i++) {
cout << 'D';
for (int j = 1; j < C; j++) cout << 'L';
cout << 'D';
for (int j = 1; j < C; j++) cout << 'R';
}
}
// 개행 문자를 출력해 출력을 종료한다.
cout << '\n';
return 0;
}'알고리즘 > 문제 풀이' 카테고리의 다른 글
| 2902번: KMP는 왜 KMP일까? (0) | 2021.12.21 |
|---|---|
| 2884번: 알람 시계 (0) | 2021.12.21 |
| 2869번: 달팽이는 올라가고 싶다 (0) | 2021.12.20 |
| 2839번: 설탕 배달 (0) | 2021.12.20 |
| 2805번: 나무 자르기 (0) | 2021.12.20 |